一、基本介绍
为避免树的高度增长过快,降低二叉排序树的性能,规定在插入和删除二叉树的结点时要保证任意结点的左、右子树的高度差的绝对值不超过 1,将这样的二叉排序树称为平衡二叉树(Balanced Binary Tree),又称AVL树。
定义结点左子树与右子树的高度差为该结点的平衡因子,则平衡二叉树结点的平衡因子的值只可能是 -1、0 或 1。
二、插入操作
二叉排序树保证平衡的基本思想为:每当在二叉排序树中插入(或删除)一个结点时,首先检查其插入路径上的结点是否因为此次操作而导致了不平衡。若导致了不平衡,则先找到插入路径上离插入结点最近的平衡因子的绝对值大于 1 的结点 N,再对以 N 为根的子树,在保持二叉排序树特性的前提下,调整各结点的位置关系,使之重新达到平衡。
平衡二叉树的调整存在LL平衡旋转(右单旋转)、RR平衡旋转(左单旋转)、LR平衡旋转(先左后右双旋转)、RL平衡旋转(先右后左双旋转)这4种情况,下面将分别介绍这几种情况下的调整方法。
(1)LL平衡旋转
假设有一颗平衡二叉树,当该二叉树插入一个结点 6 时,根节点的平衡因子的绝对值大于 1,此时该二叉树不再是一颗平衡二叉树,如下图所示:
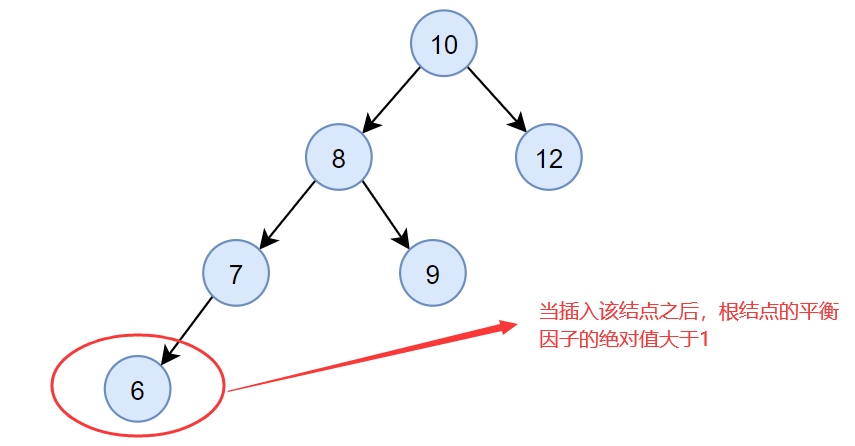
可以看到,由于在结点10的左孩子(结点8)的左子树上插入了一个新结点(结点6),结点10的平衡因子由 1 增至 2,导致以结点10为根的子树失去平衡,因此需要一次向右的旋转操作。
【操作步骤】
- 首先创建一个新结点,并将新结点的值设置为根结点的值
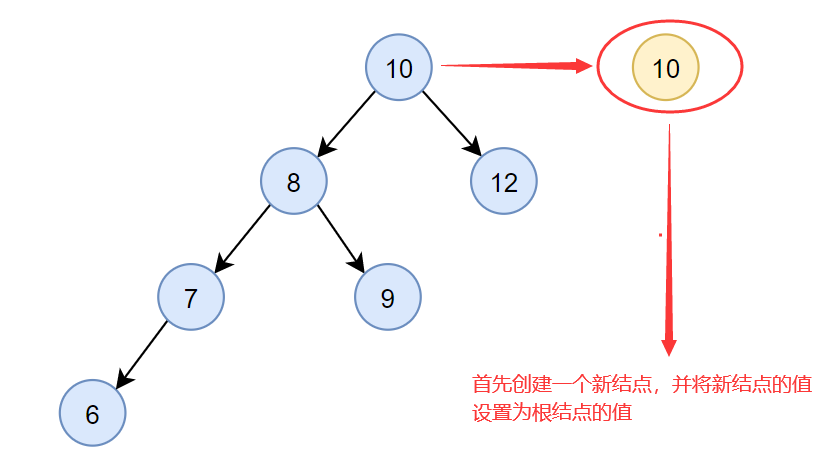
- 之后将新结点的左孩子设置为根结点的左孩子的右子树,将新结点的右孩子设置为根结点的右孩子
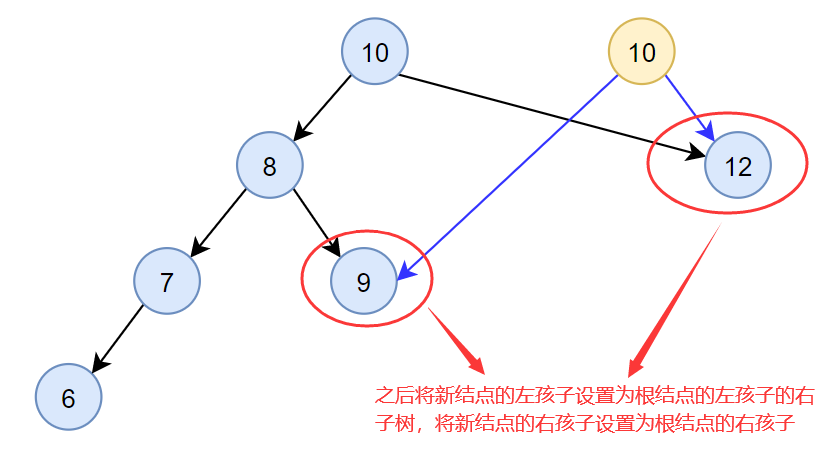
- 然后将根结点的值设置为其左孩子的值,并将根结点的右孩子设置为新结点
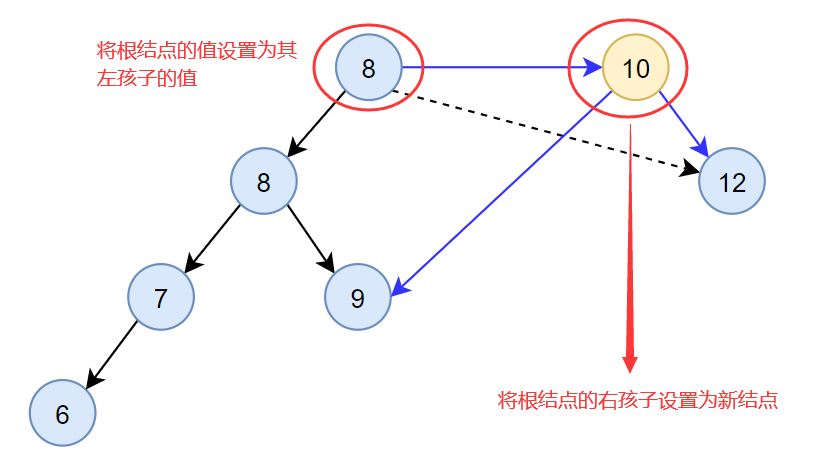
- 最后将根结点的左孩子设置为其左孩子的左子树
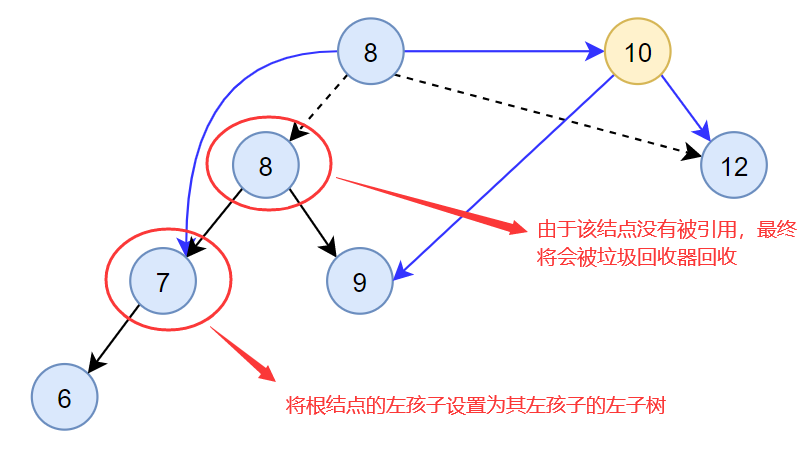
【实现效果】
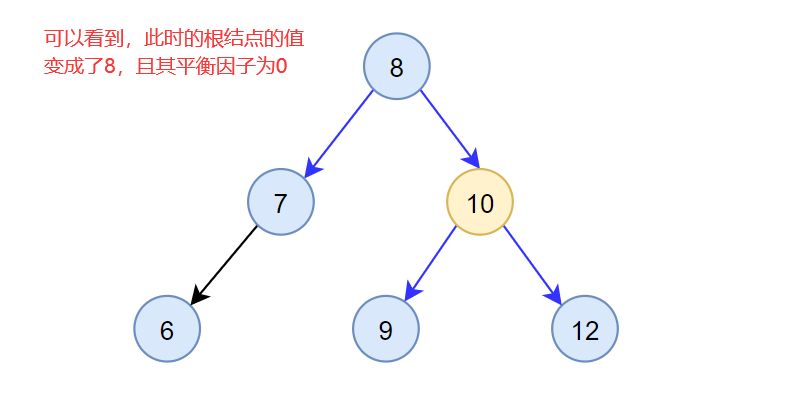
可以看到,此时的根结点的值为8,原根结点10移动到现根结点8的右侧,相当于进行了一次向右旋转。
【代码实现】
1 | // LL平衡旋转 |
(2)RR平衡旋转
假设有一颗平衡二叉树,当该二叉树插入一个结点 8 时,根节点的平衡因子的绝对值大于 1,此时该二叉树不再是一颗平衡二叉树,如下图所示:
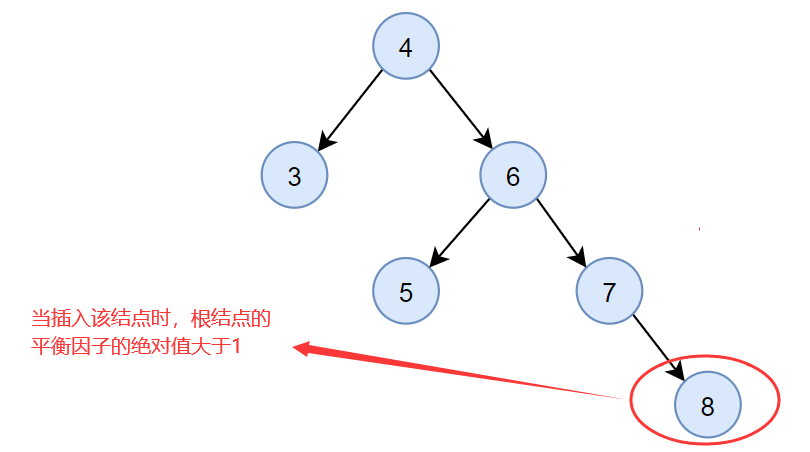
可以看到,由于在结点4的右孩子(结点6)的右子树上插入了一个新结点(结点8),结点4的平衡因子由 -1 减至 -2,导致以结点4为根的子树失去平衡,因此需要一次向左的旋转操作。
【操作步骤】
- 创建新的结点,并将新结点的值设置为根结点的值
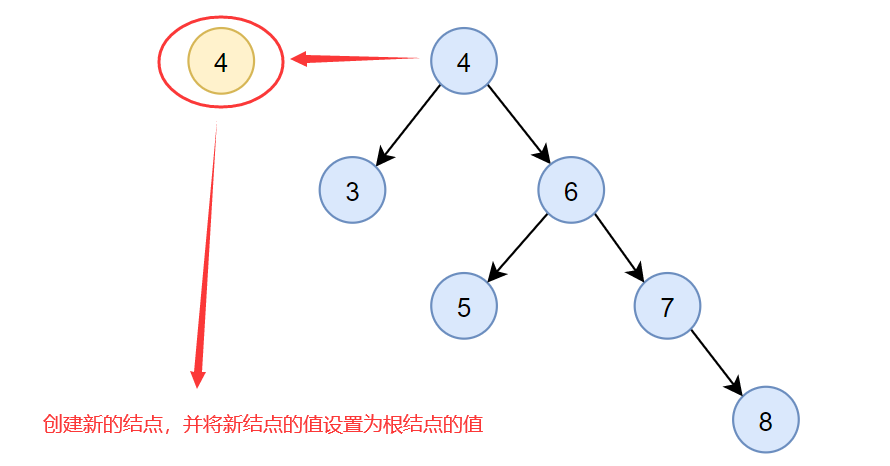
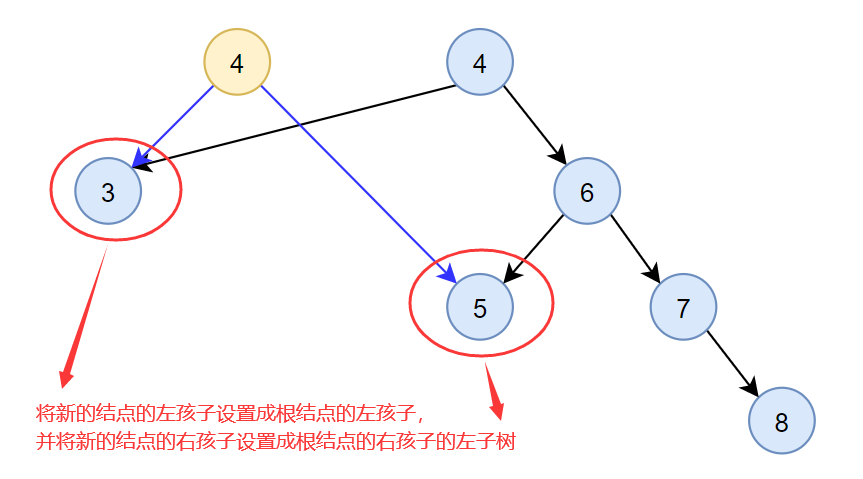
- 将新的结点的左孩子设置成根结点的左孩子,并将新的结点的右孩子设置成根结点的右孩子的左子树
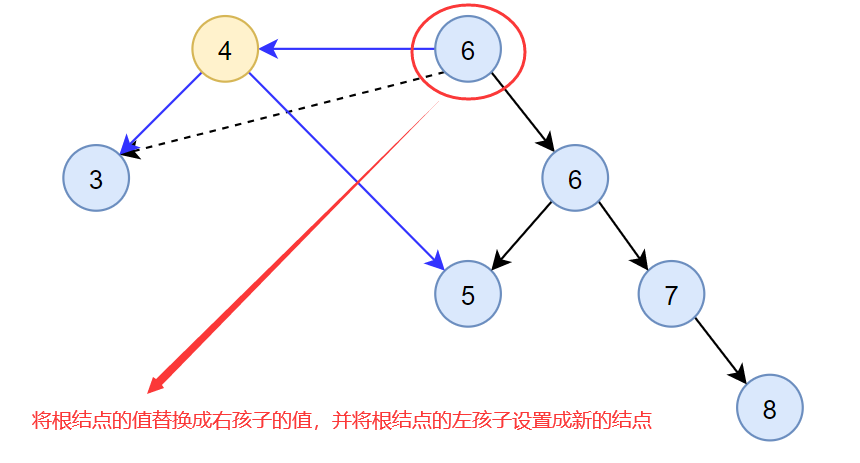
- 将根结点的值替换成右孩子的值,并将根结点的左孩子设置成新的结点
- 将根结点的右孩子设置成右孩子的右子树
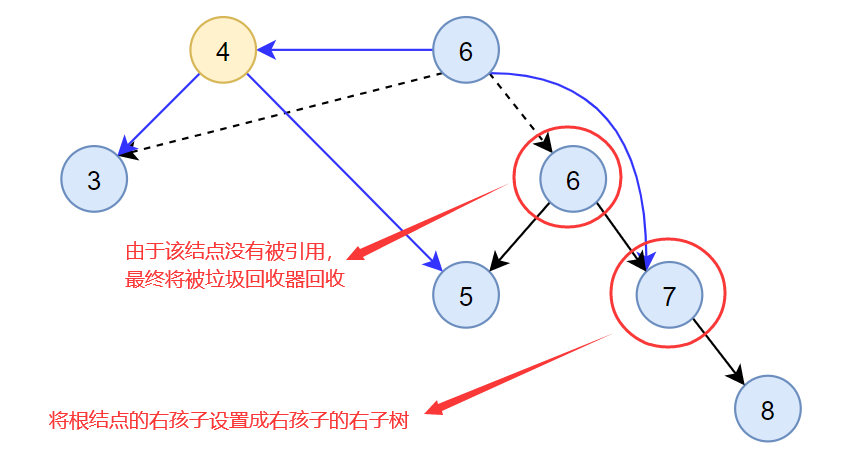
【实现效果】
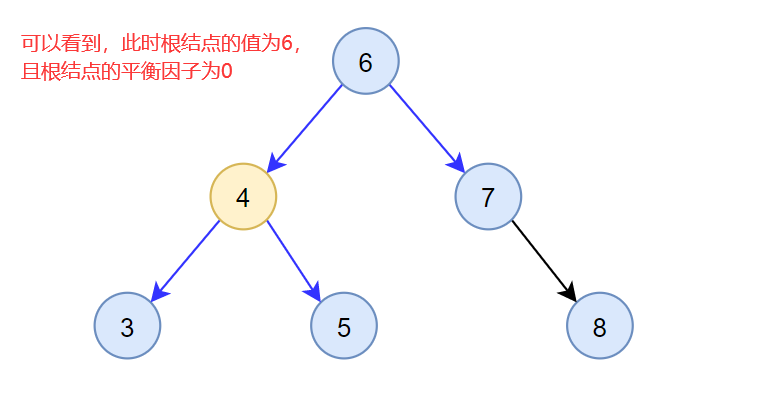
可以看到,此时的根结点的值为6,原根结点4移动到现根结点6的左侧,相当于进行了一次向左旋转。
【实现代码】
1 | // RR平衡旋转 |
(3)LR平衡旋转
假设有一颗平衡二叉树,如下图(a)所示,当插入结点9后根结点的平衡因子为2,因此需要进行调整。如果我们直接进行RR平衡旋转,得到的结果如下图(b)所示,此时根结点的平衡因子为-2,仍然不是一颗平衡二叉树。
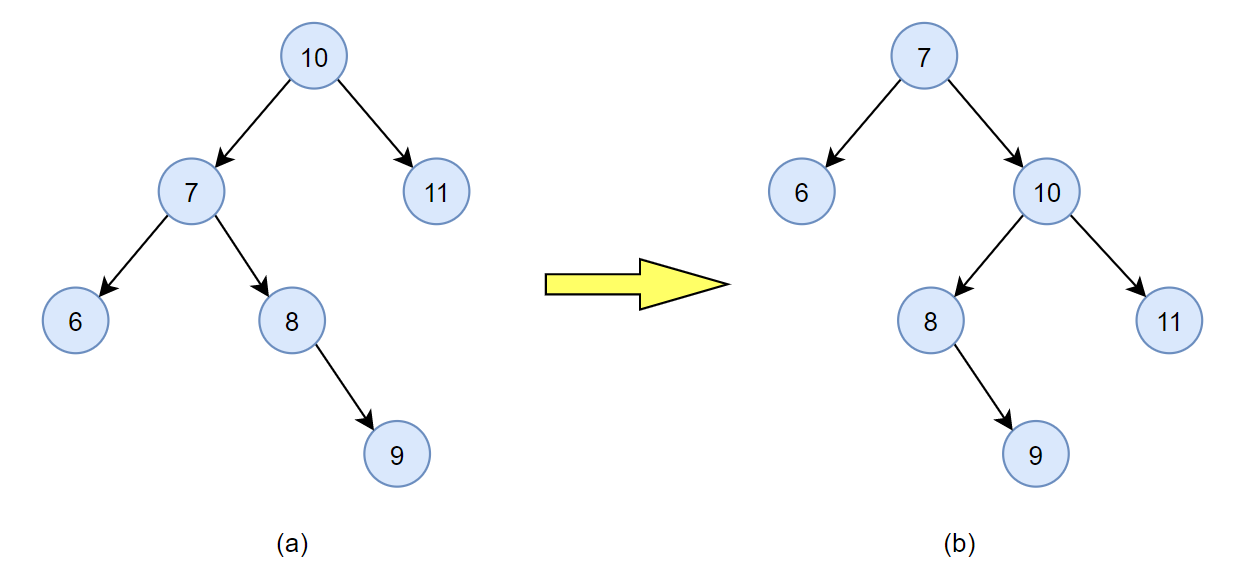
那么该如何调整上面的二叉树,使其成为一颗平衡二叉树呢?
首先通过观察,我们可以发现上图(a)中根结点的左孩子的右子树高度大于根结点的左孩子的左子树的高度,对于这种情况,我们可以先对根结点的左孩子进行RR平衡旋转,再对根结点进行LL平衡旋转,即LR平衡旋转。
【操作步骤】
- 先将根结点的左孩子进行RR平衡旋转
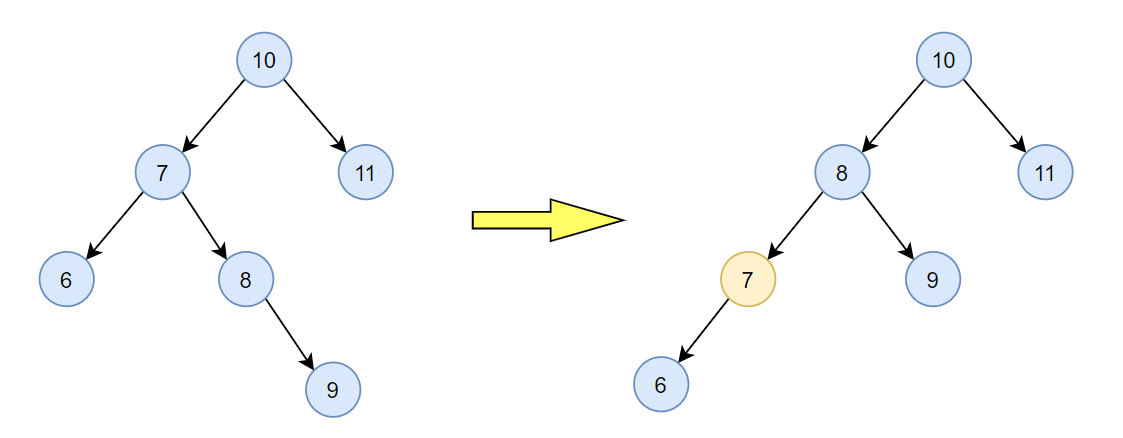
- 再将根结点进行LL平衡旋转
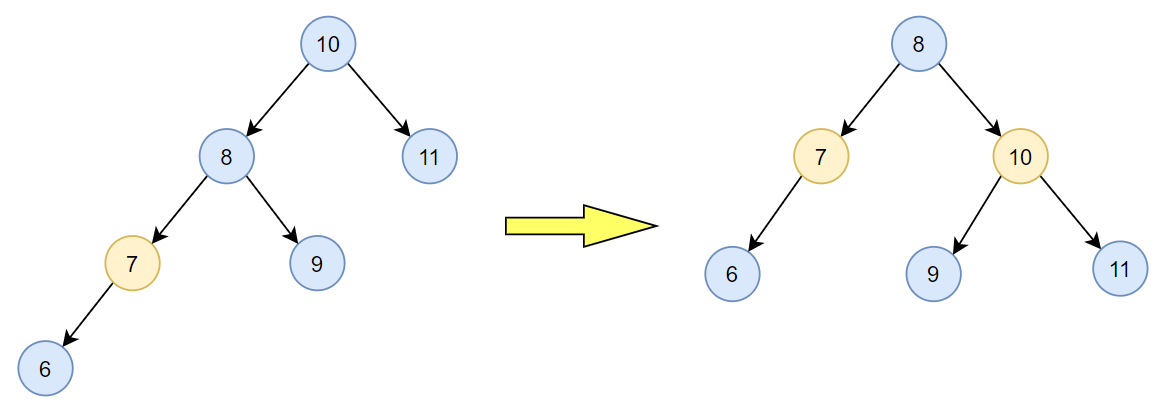
(4)RL平衡旋转
与LR平衡旋转类似,当根结点的右孩子的左子树高度大于根结点的右孩子的右子树的高度时,我们可以先对根结点的右孩子进行LL平衡旋转,再对根结点进行RR平衡旋转,即RL平衡旋转。
【操作步骤】
假设有一颗平衡二叉树 {2, 1, 6, 5, 7},在插入结点3后,可根据如下步骤进行调整:
- 先将根结点的左孩子进行RR平衡旋转
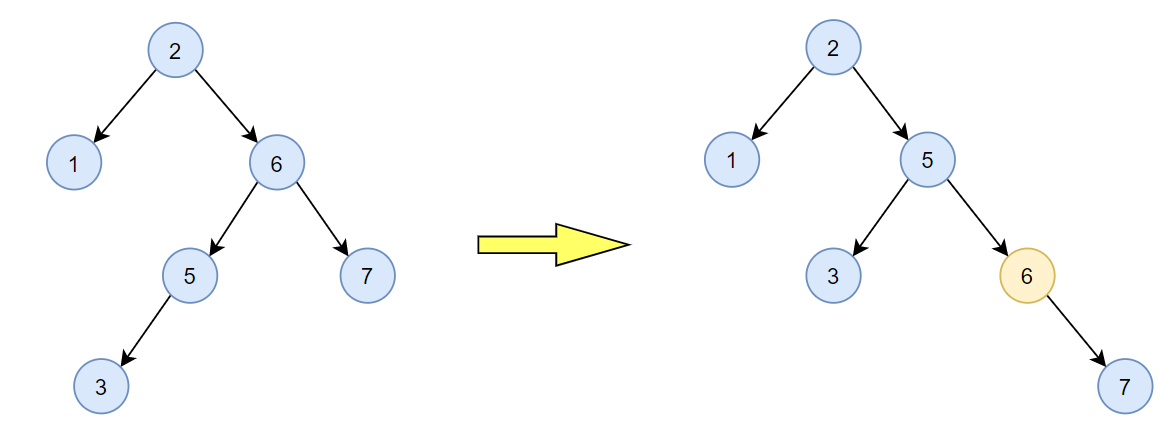
- 再将根结点进行LL平衡旋转
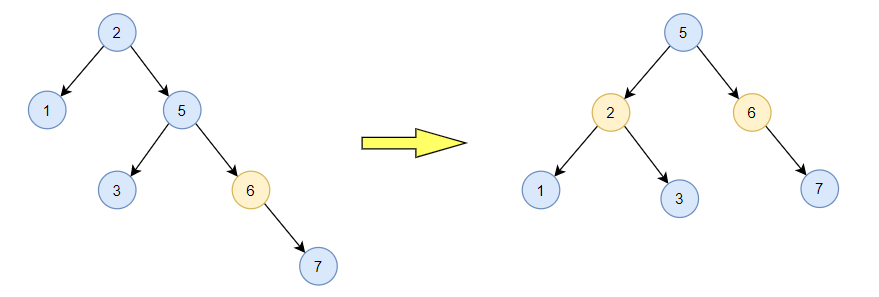
三、查找操作
平衡二叉树的查找操作与二叉排序树相同,详细内容可阅读我之前写的一篇文章《二叉排序树》,这里不再进行赘述。这里需要注意的是,平衡二叉树在二叉排序树的基础上进行了优化,解决了极端情况下(二叉树变成了单链表)查找效率降低的问题。因此平衡二叉树的平均查找长度为$O(log_2n)$。
四、完整实现
1、获取二叉树的高度
在实现平衡二叉树的操作之前我们需要获取二叉树的高度,因为只有知道了树的高度才能判断在插入一个新结点后该树是否仍为平衡二叉树。因此我们需要在TreeNode类中添加以下方法:
1 | // 返回当前结点的左子树的高度 |
2、在插入时进行平衡旋转
当可以获取二叉树的高度之后,就可以在TreeNode类插入结点方法中添加以下内容:
1 | public void add(TreeNode node) { |
完整的实现代码已上传到Gitee,仓库地址:https://gitee.com/fzcoder/data-structure-and-algorithms-demo。