归并排序 | Frank's Blog

一、基本概念

归并排序（Merge Sort） 是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer） 的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

二、具体实现

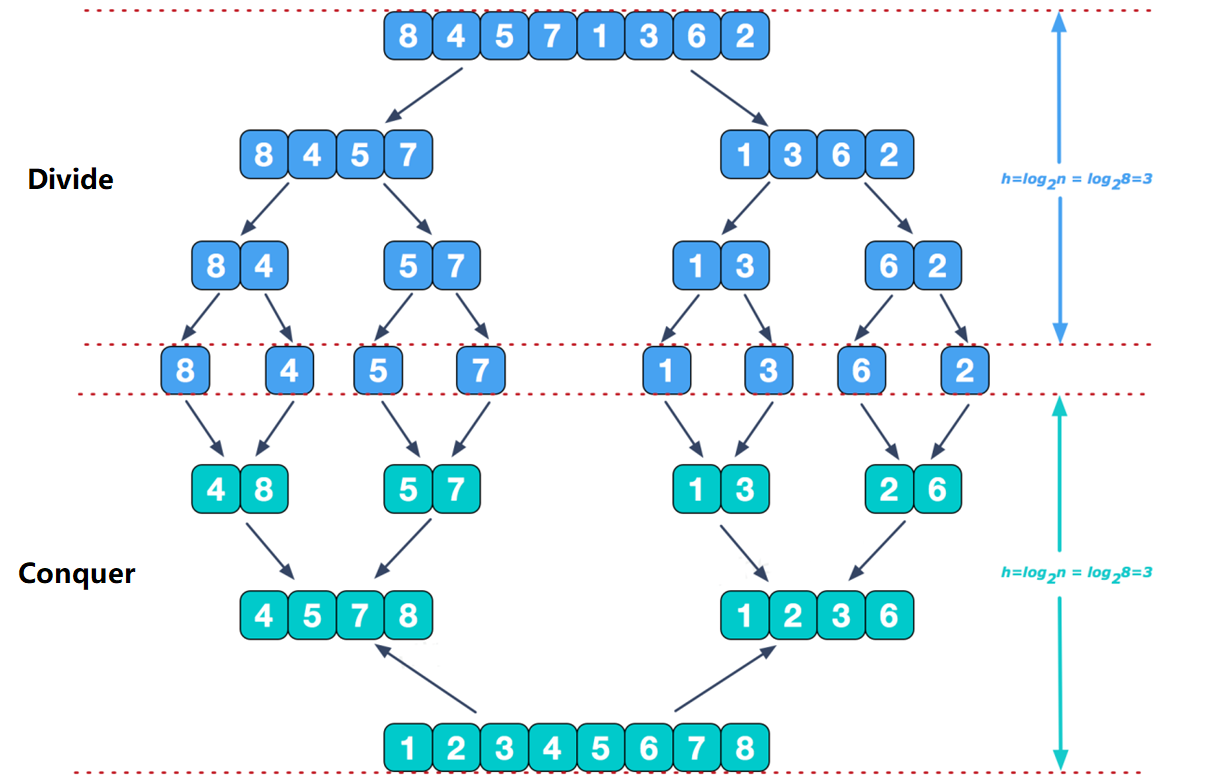
1、divide

分（divide）的过程很简单，只需不断的从中间划分序列即可。代码实现如下：

public static void mergeSort(int[] arr, int low, int high, int[] temp) {
    if (low < high) {
        // 从中间划分两个子序列
        int mid = (low + high) / 2;
        // 对左侧子序列进行递归排序
        mergeSort(arr, low, mid, temp);
        // 对右侧子序列进行递归排序
        mergeSort(arr, mid + 1, high, temp);
        // 归并
        merge(arr, low, mid, high, temp);
    }
}

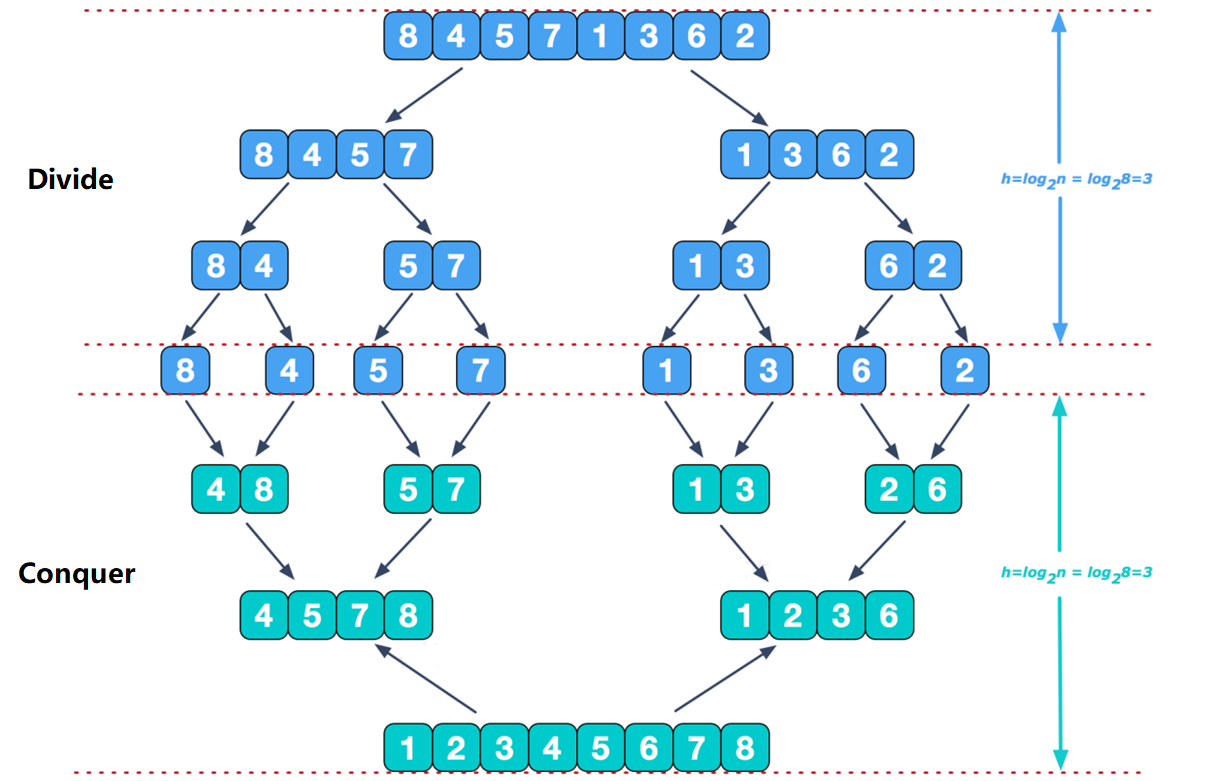
2、conquer

在治（conquer）的阶段需要将两个已经有序的子序列合并成一个有序序列。例如上图中的最后一次合并，要将${4,5,7,8}$和${1,2,3,6}$两个已经有序的子序列，合并为最终序列${1,2,3,4,5,6,7,8}$，下面将介绍具体的实现步骤：

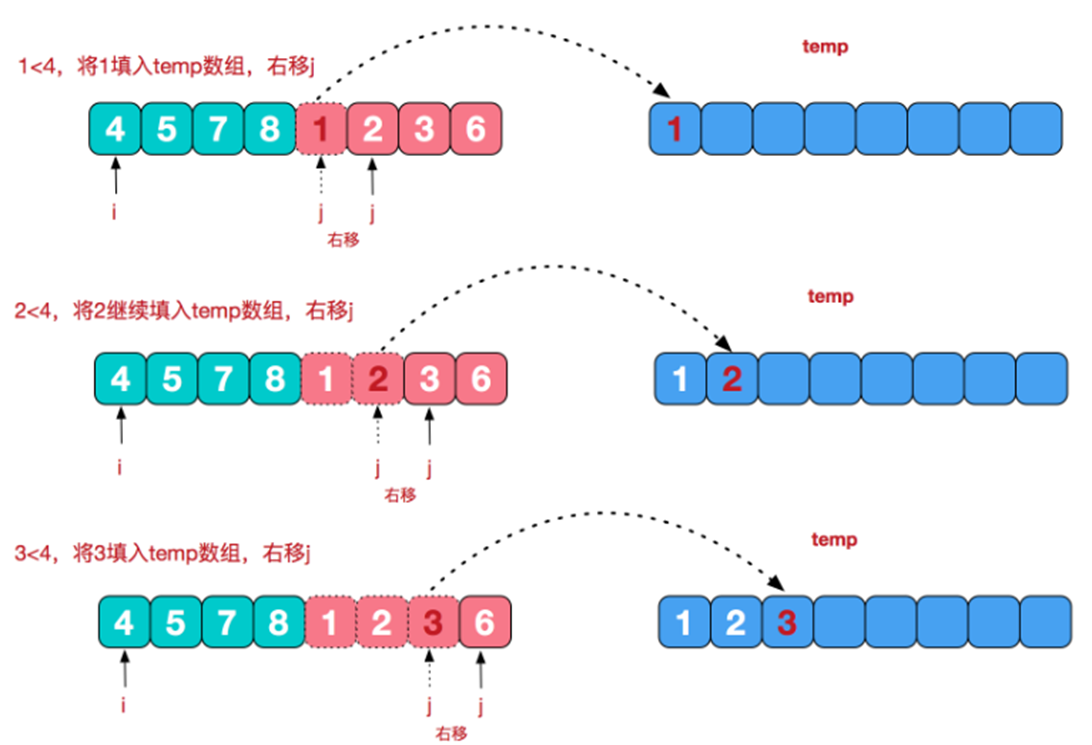
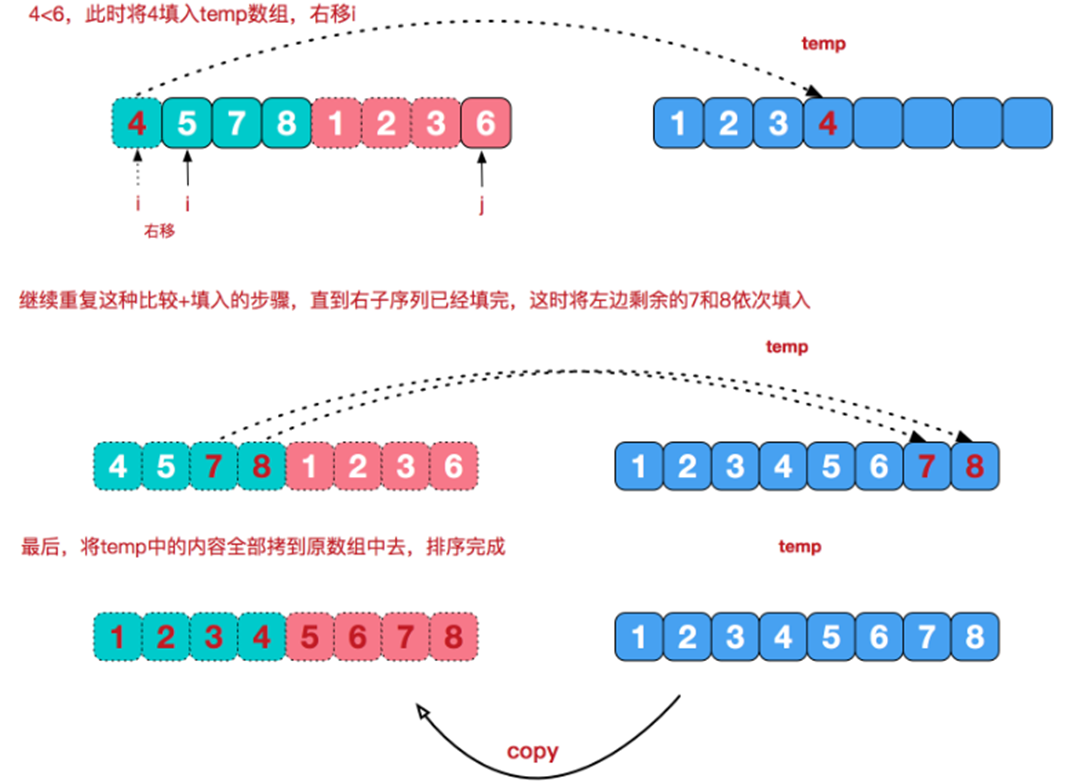
代码实现如下：

public static void merge(int[] arr, int low, int mid, int high, int[] temp) {
    int i = low; // 初始化i，左边有序序列的初始索引
    int j = mid + 1; // 初始化j，右边有序序列的初始索引
    int t = 0; // 指向辅助数组的当前索引
    // 1.将左右两边的数据按规则添加到辅助数组中
    while (i <= mid && j <= high) {
        if (arr[i] < arr[j]) {
            temp[t++] = arr[i++];
        } else {
            temp[t++] = arr[j++];
        }
    }
    // 2.将有剩余数据的一边依次添加到辅助数组中
    // 注意: 下面的两个while循环最多只会执行其中一个
    while (i <= mid) {
        temp[t++] = arr[i++];
    }

    while (j <= high) {
        temp[t++] = arr[j++];
    }
    // 3.保存辅助数组的当前长度并将指针初始化
    int len = t;
    t = 0;
    // 4.将辅助数组中的数据复制到原数组中
    while (t < len) {
        arr[low + t] = temp[t];
        t++;
    }
}