一、基本概念
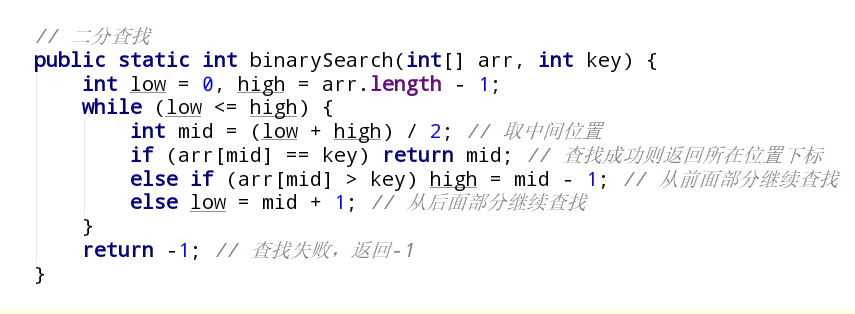
快速排序(Quick Sort) 的基本思想是基于分治法的,该算法通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
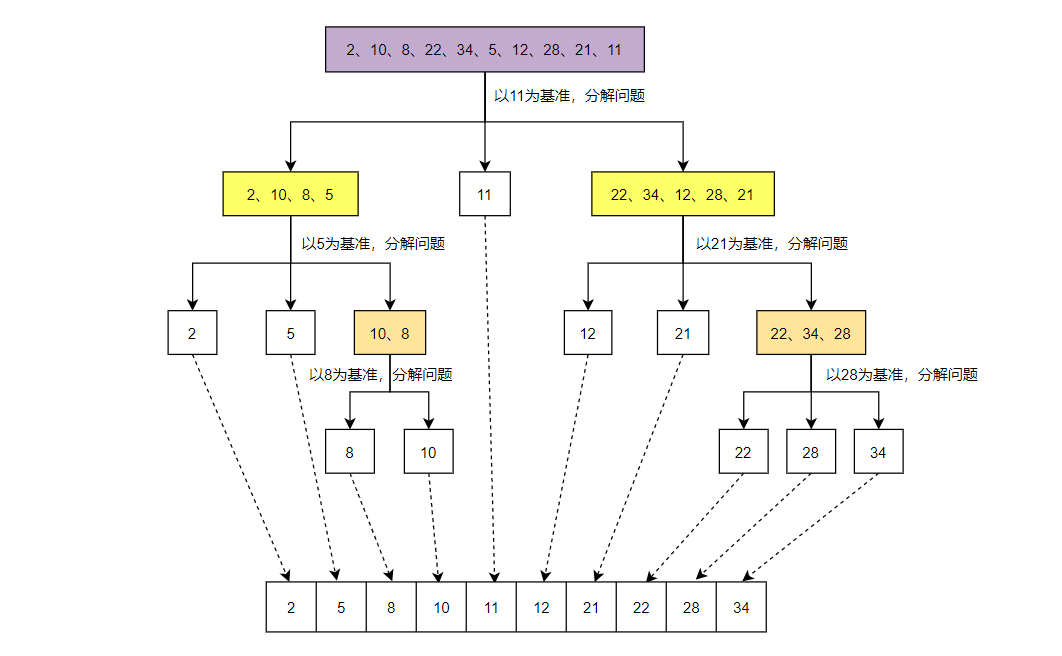
二、具体实现
由上图可知,在每一趟快速排序中,都需要选择一个元素将待排序表划分为两部分,这个用来划分待排序表的元素叫做主元(pivot element),或者叫做基准。一趟快速排序的过程是一个交替搜索和交换的过程,下面通过实例来进行介绍。
1、操作过程
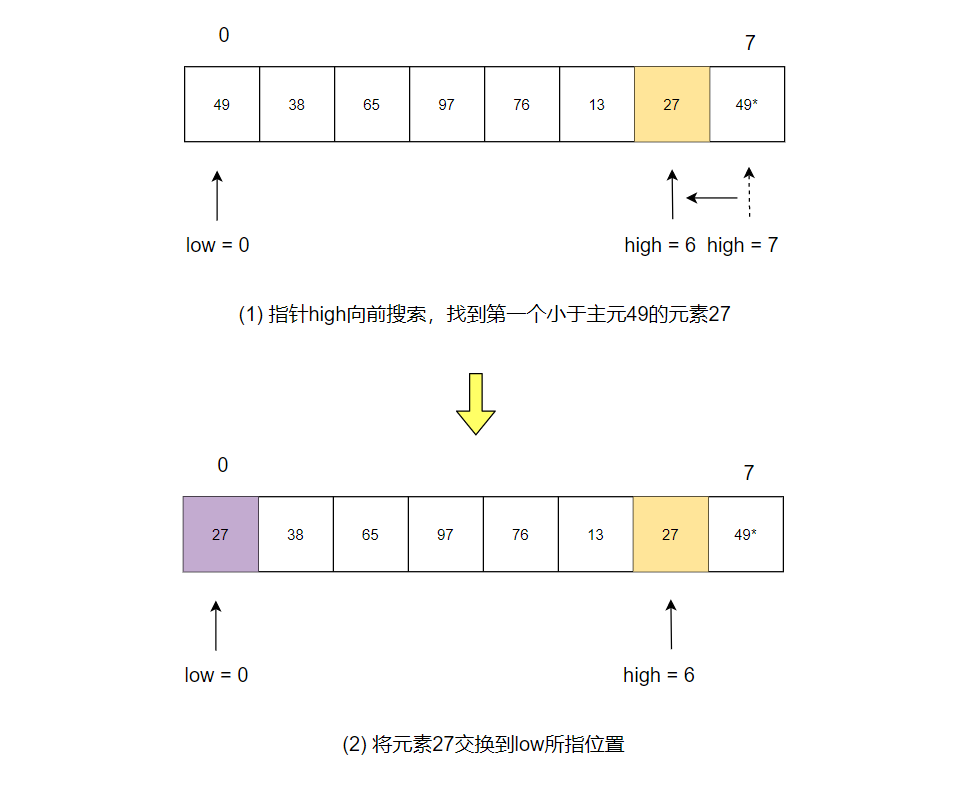
假设有一个待排序的数组$= {49, 38, 65, 97, 76, 13, 27}$,我们选择数组的首个元素 49 作为主元,下面是一趟快速排序的过程:
- 指针 high 向前搜索,找到第一个小于主元49的元素27,并将其交换到 low 所指位置
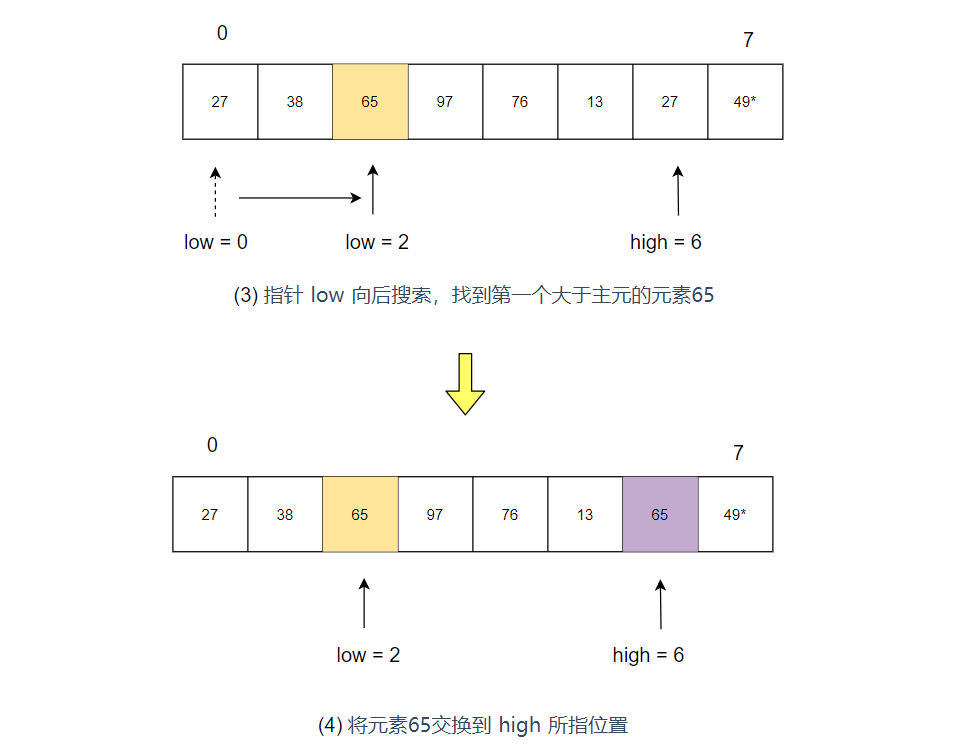
- 指针 low 向后搜索,找到第一个大于主元49的元素65,并将其交换到 high 所指位置
- 指针 high 继续向前搜索找到第一个小于主元49的元素13,并将其交换到 low 所指位置
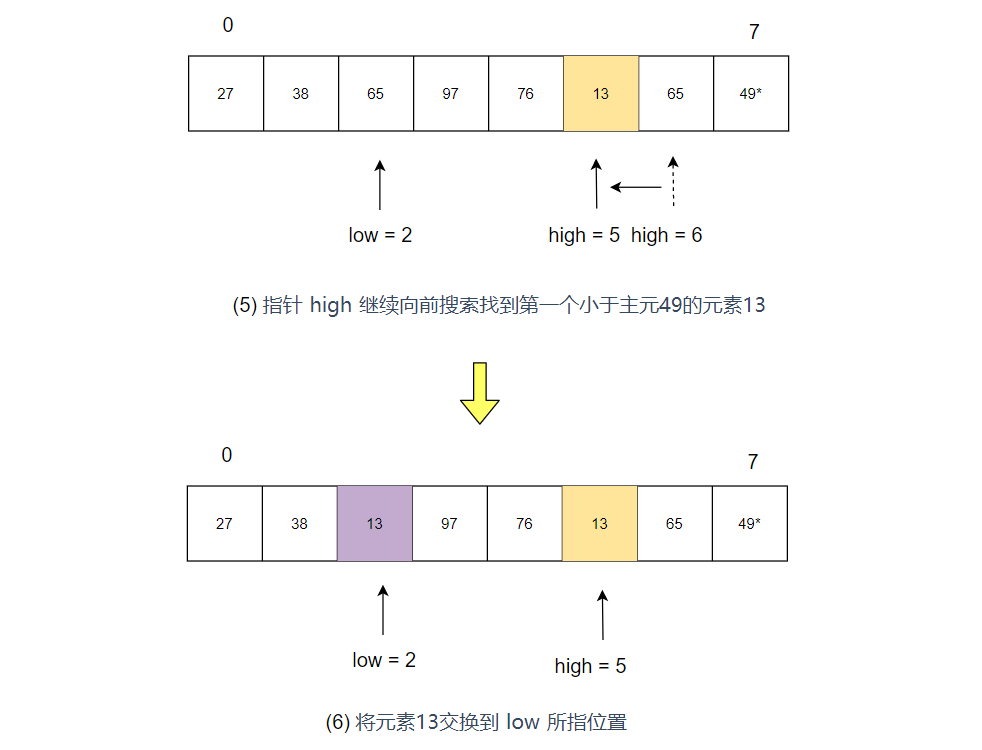
- 指针 low 向后搜索,找到第一个大于主元49的元素97,并将其交换到 high 所指位置
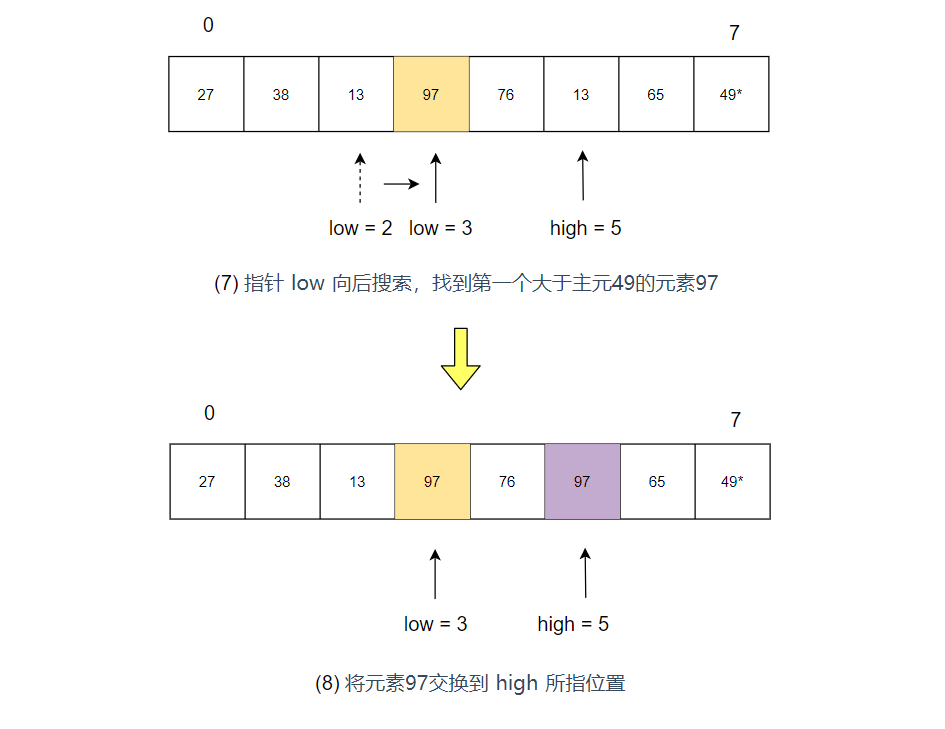
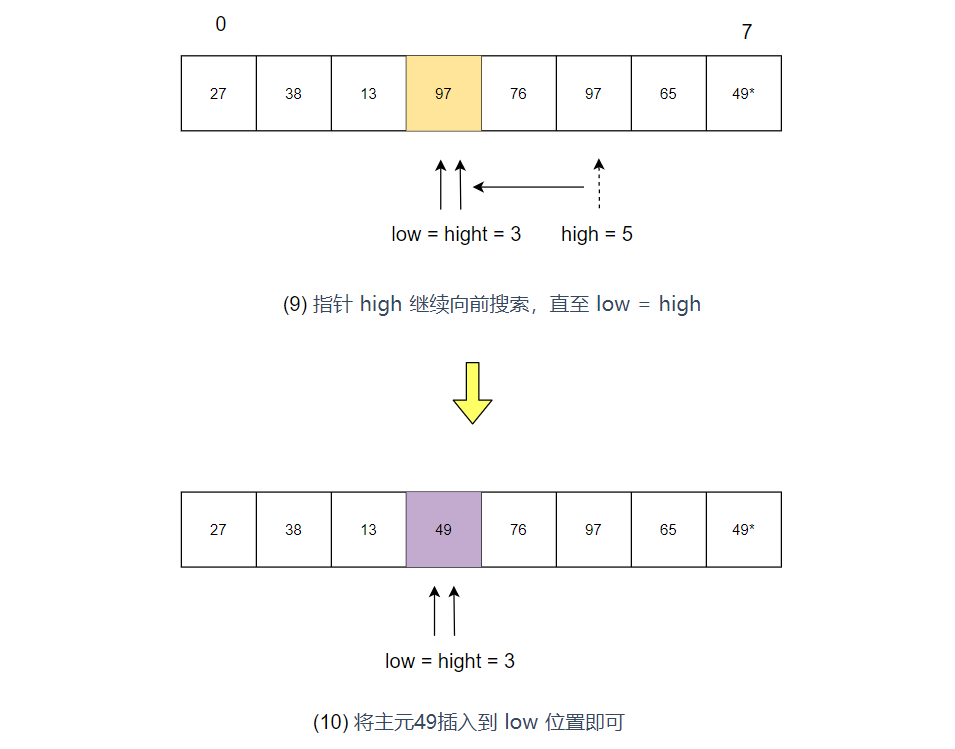
- 指针 high 继续向前搜索,直至$low = high$,之后将主元插入到 low 位置即可
2、代码实现
由上文可知,在每趟快速排序时需要一个划分算法对待排序的列表进行划分操作,之后对每块划分的区域再进行快速排序,因此可采用递归来实现快速排序算法,代码如下:
1 | public static void quickSort(int[] arr, int low, int high) { |
其中划分算法如下:
1 | public static int partition(int[] arr, int low, int high) { |
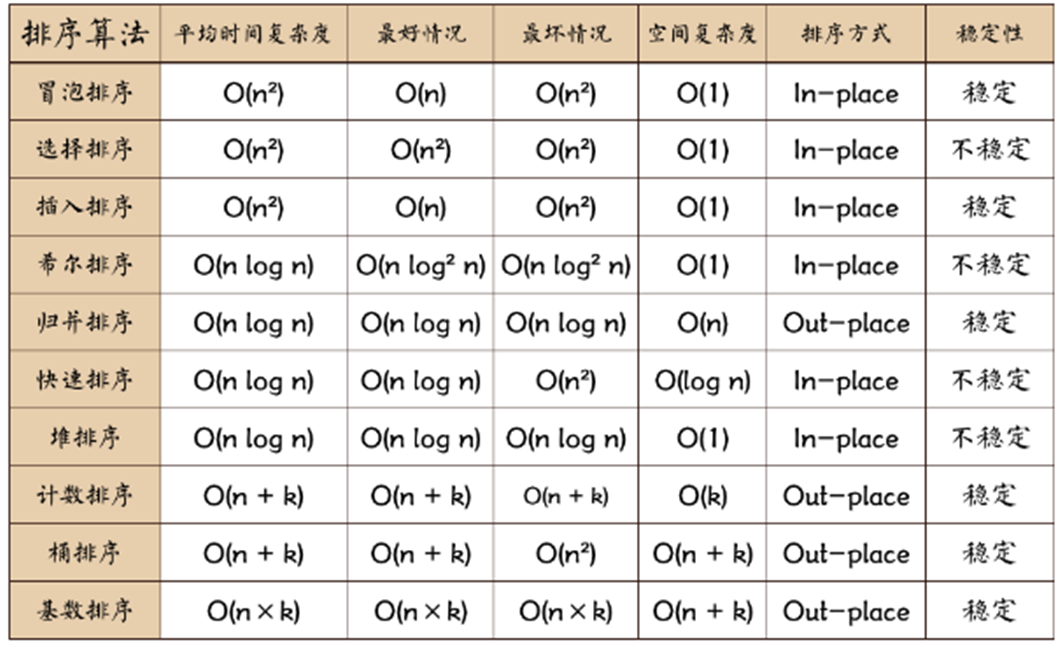
三、性能分析
1、时间效率
快速排序的运行时间与划分是否对称有关。快速排序的最坏情况发生在两个区域分别包含 $n-1$ 和 0 个元素时,若每层递归都会出现这种情况,则时间复杂度为$O(n^2)$;若划分的比较平衡,此时的时间复杂度为$O(nlog_2n)$。快速排序在一般情况下与其最佳情况下的运行时间很接近。快速排序是所有内部排序算法中平均性能最优的排序算法。
2、空间效率
最好情况下为$O(log_2n)$,最坏情况下为$O(n)$ ,平均情况下为$O(log_2n)$ 。
3、稳定性
在划分算法中,若右端区域有两个关键字相同,且小于基准值的记录,则在交换到左端区间后,它们的相对位置会发生变化,即快速排序是一种不稳定的排序方法。