一、基本概念
1、堆
堆(heap) 是一个数组,它可以被看成一个近似的完全二叉树。树上的每一个结点对应数组中的一个元素,除最底层外,该树是完全充满的,而且是从左向右填充的。
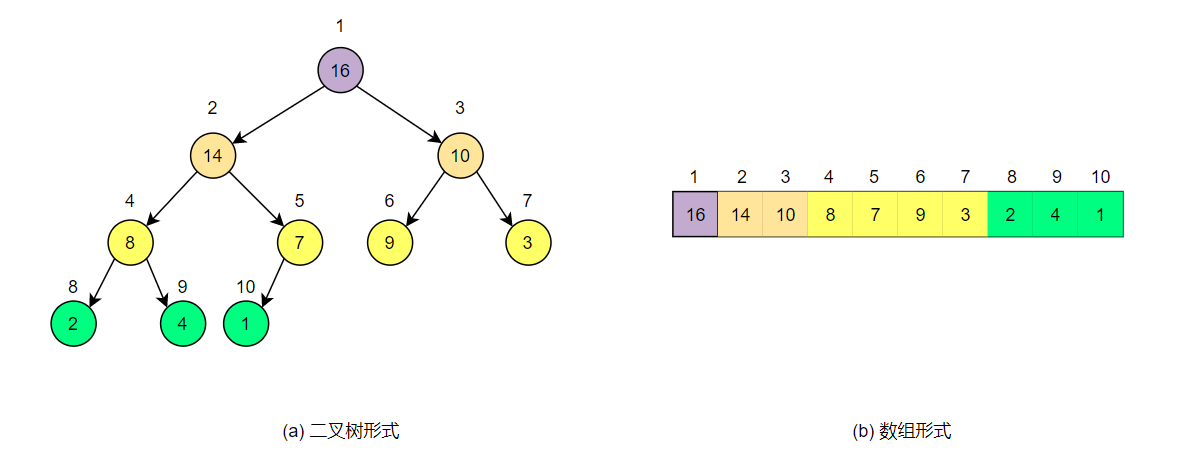
二叉堆可以分为两种形式:最大堆和最小堆。在这两种堆中,结点的值都要满足堆的性质,但一些细节定义则有所差异。在最大堆中,最大堆性质是指除了根以外的所有结点都要满足$parent.val \ge node.val$,也就是父结点大于等于子结点;而最小堆正好相反,即除了根以外的所有结点都要满足$parent.val \le node.val$,也就是父结点小于等于子结点。
2、堆排序
堆排序(heap sort),顾名思义,就是一种通过堆实现排序的算法,在堆排序中使用的是最大堆。堆排序的基本思想如下:
- 将待排序的序列构造成一个最大堆,此时整个序列的最大值就是堆顶的根节点。
- 将其与末尾元素进行交换,此时末尾就为最大值。
- 然后将剩余$n-1$个元素重新构造成一个最大堆, 这样会得到剩余$n-1$个元素的最大值。
- 如此反复执行,便能得到一个有序的序列。
接下来我们将介绍堆排序的具体实现。
二、具体实现
1、建堆
首先我们需要做的就是将无需的序列建立一个初始堆(升序采用最大堆,降序采用最小堆),下面将结合实例来分析建堆的过程。
假设存在一个无序序列,该序列的二叉树形式和数组形式如下:
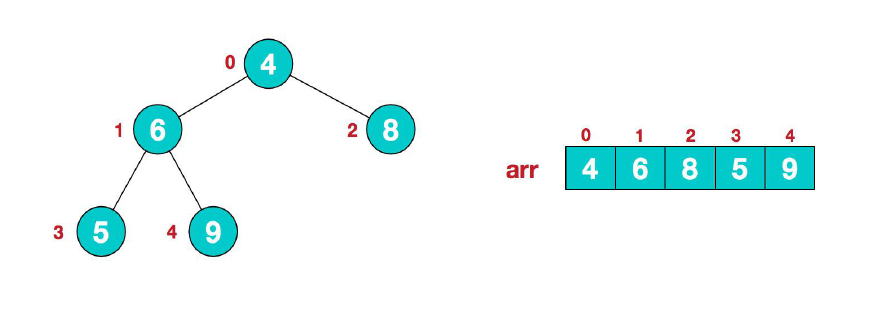
(1) 首先我们从最后一个非叶子结点开始(叶结点不需要调整,第一个非叶子结点$arr.length/2-1=5/2-1=1$,也就是结点6),从左至右,从下至上进行调整。
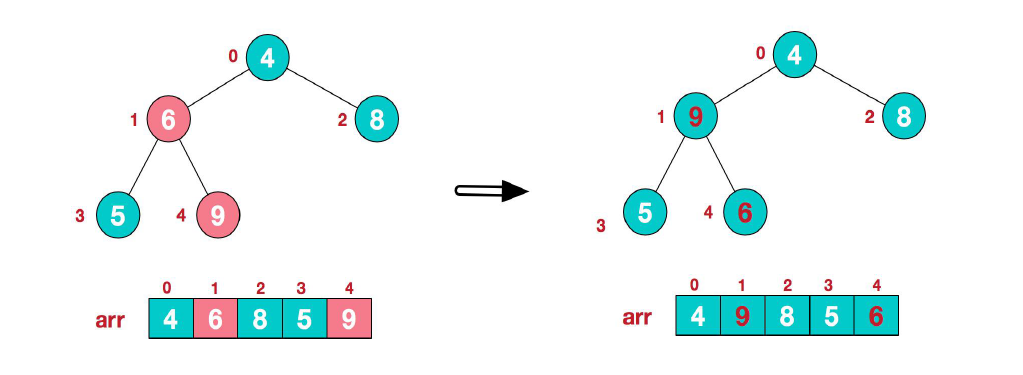
(2) 接下来找到第二个非叶子结点 4,由于在${4,9,8}$中结点 9 最大,因此将结点 4 和结点 9 交换。
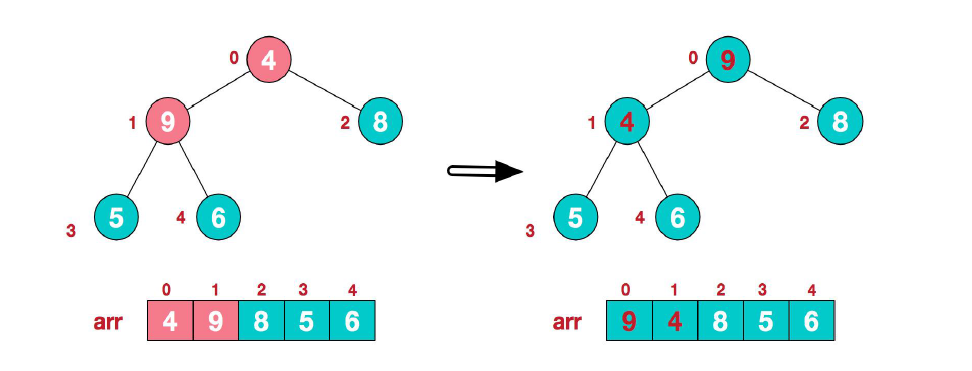
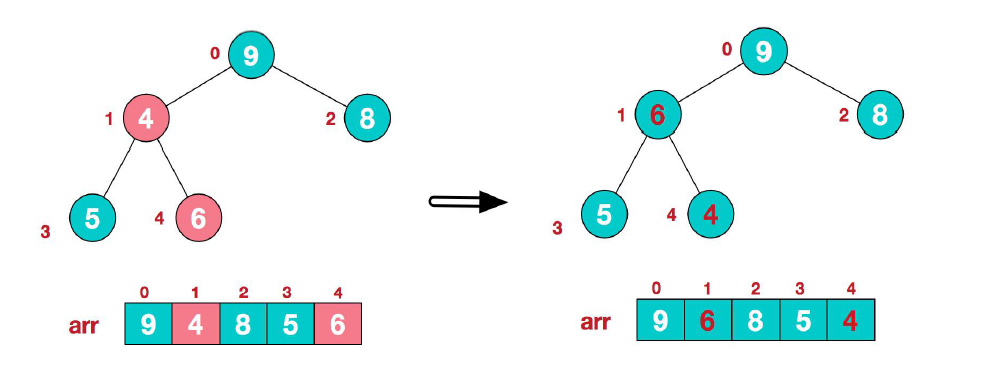
(3) 然而上面的交换导致了子树中${4, 5,6}$不满足最大堆的要求,因此继续调整,在${4, 5,6}$中结点 6 最大,所以交换结点 4 和结点 6。此时,我们就将一个无序序列构造成了一个最大堆。
2、调整堆
在建好一个初始堆之后,需要将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行,直至将序列变成一个有序序列。下面将接着上面的例子来分析具体的过程。
(1) 首先,将堆顶元素 9 和末尾元素 4 进行交换。
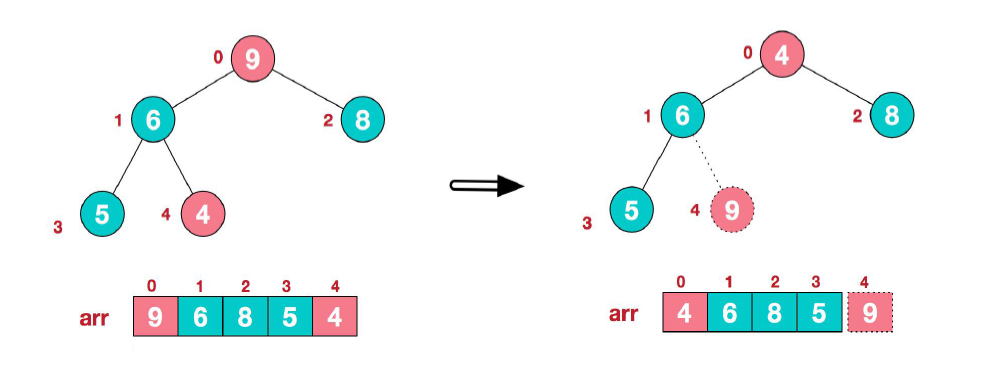
(2) 重新调整结构,使其继续满足堆定义。
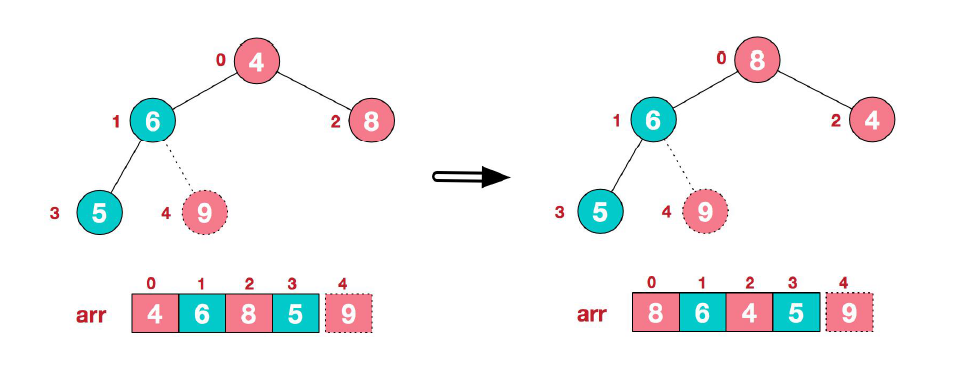
(3) 再将堆顶元素 8 与末元素 5 进行交换,得到第二大元素 8。
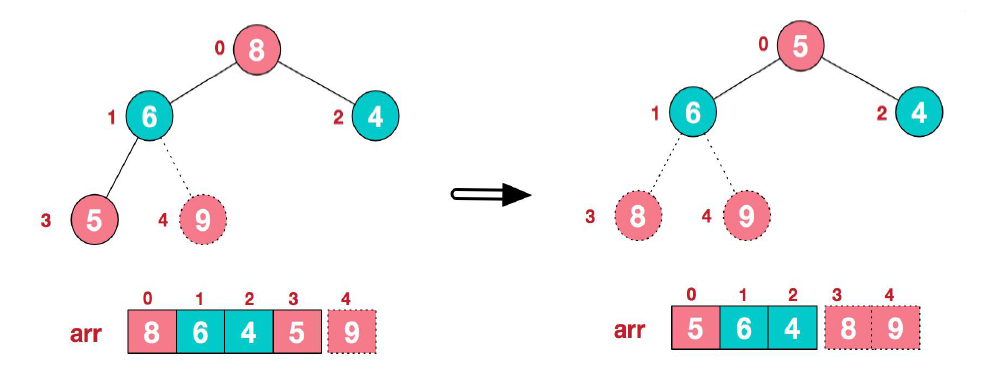
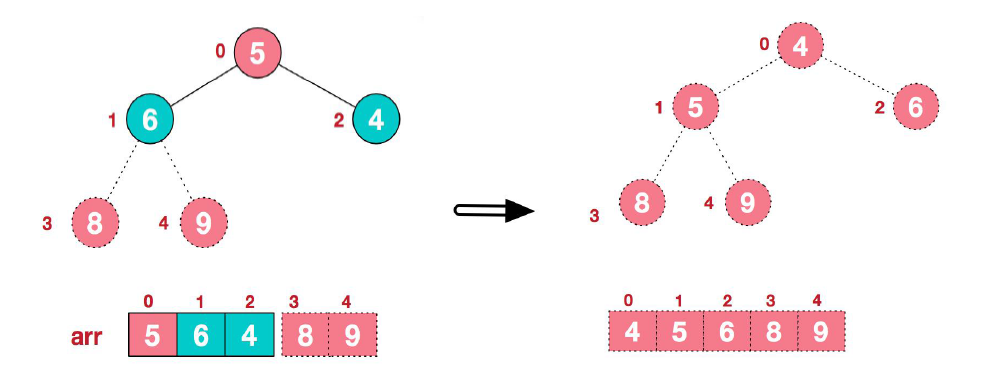
(4) 继续进行调整,如此反复进行,最终使得整个序列有序。
3、代码实现
堆排序采用Java语言的完整实现已上传Gitee,项目地址:https://gitee.com/fzcoder/data-structure-and-algorithms-demo,下面给出部分算法的实现。
(1) 堆排序算法
1 | public static void heapSort(int[] arr) { |
(2) 对以下标为 index 的根结点的子树进行调整
1 | public static void adjustHeap(int[] arr, int index, int length) { |
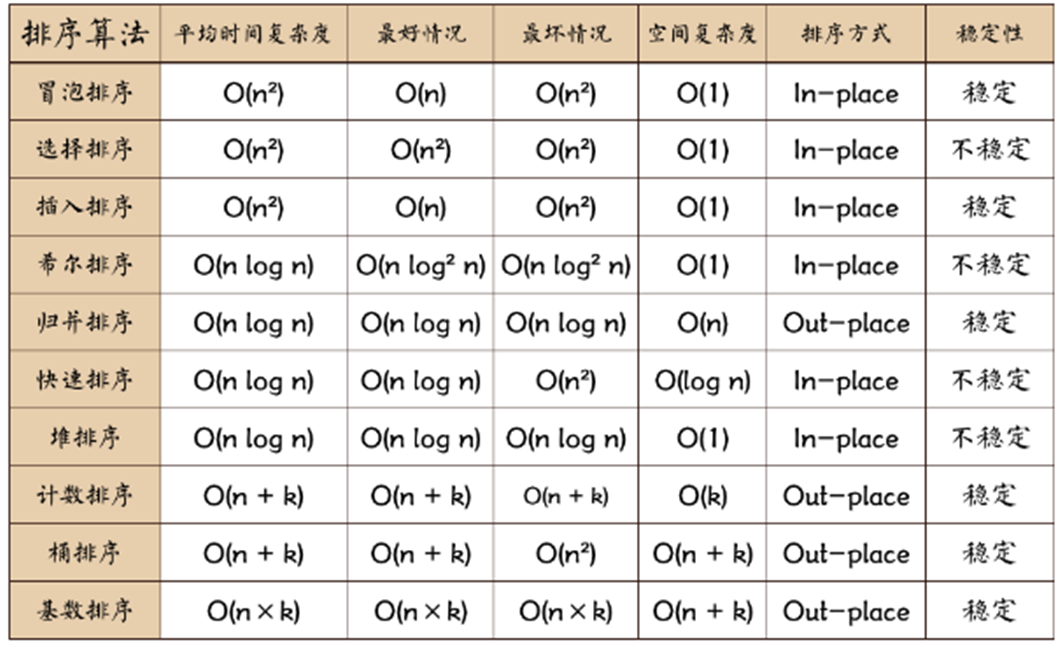
三、性能分析
1、时间效率
建堆时间为$O(n)$,之后有$n-1$次向下调整操作,每次调整的时间复杂度为$O(h)$。因此在最好、最坏和平均情况下,堆排序的时间复杂度为$O(nlog_2n)$。
2、空间效率
仅使用了常数个辅助单元,所以空间复杂度为$O(1)$。
3、稳定性
进行筛选时,有可能把后面相同关键字的元素调整到前面,所以堆排序算法是一种不稳定的排序方法。